Éditions Hatier, Paris, 2023
quiz

Quiz du chapitre 6

Pour chaque question, cochez la ou les réponse(s) exacte(s) :

  1. A. Dans ce qui suit, f est une fonction définie sur I et F une primitive de f sur I.

    1. f (x) = −2x + 1, I = ℝ, alors :

    002x
    • F(x) = −2.
    • F(x) = −x2 + x.
    • F(x) = −x2 + x + 1.

  2. 2. f(x) = −x2 + x + 1, I = ℝ, alors :

    003x
    • F(x) = −13\frac{1}{3}x3 − x2.
    • F(x) = −13\frac{1}{3}x3 − x2 + 1.
    • F(x) = −13\frac{1}{3}x3 − x2 + x + 1.

  3. 3. f(x) = x − 1x2\frac{1}{x^{2}} , I = ]0, +∞[, alors :

    001x
    • F(x) = 12\frac{1}{2}x2 + 1x\frac{1}{x}.
    • F(x) = 1 + 2x3\frac{2}{x^{3}}.
    • F(x) = 12\frac{1}{2}x2 − 1x\frac{1}{x}.

  4. 4. f(x)= cos2x, I = ℝ, alors :

    002x
    • F(x)= −sin2x.
    • F(x)= 12\frac{1}{2}sin2x.
    • F(x)= −12\frac{1}{2}sin2x.

  5. 5. f(x)= x − 3 + ex , I = ℝ, alors :

    002x
    • F(x) = 1 + ex.
    • F(x) = 12\frac{1}{2}x2 − 3x + ex.
    • F(x) = 12\frac{1}{2}x2 − 3 + ex.

  6. 6. f (x) = 2x + 1 + 1x\frac{1}{x}, I = ]0, +∞[, alors :

    002x
    • F(x) = 2 − 1x2\frac{1}{x^{2}}.
    • F(x) = x2 + x + lnx.
    • F(x) = 12\frac{1}{2}x2 + x − 1x2\frac{1}{x^{2}} .

  7. B. On considère la fonction f définie sur ]0, +∞[ par f(x) = lnx. La primitive F de f sur ]0, +∞[ telle que F(1) = 3 est donnée par :

    004x
    • F(x) = xlnx − 2x + 5.
    • F(x) = 3x\frac{3}{x}.
    • F(x) = xlnx + 3.
    • F(x) = xlnx − x + 5..

  8. C.1. f(x) = x − 3, alors :

    003x
    • ∫13f(x)dx\int_{1}^{3}f(x)dx = 2.
    • ∫13f(x)dx\int_{1}^{3}f(x)dx = 1.
    • ∫13f(x)dx\int_{1}^{3}f(x)dx = −2.

  9. 2. f(x) = x + 1x\frac{1}{x}, alors :

    001x
    • ∫1ef(x)dx=e22+12\int_{1}^{e}f(x)dx = \frac{e^{2}}{2} + \frac{1}{2}.
    • ∫1ef(x)dx=e\int_{1}^{e}f(x)dx = e.
    • ∫1ef(x)dx=12e+12\int_{1}^{e}f(x)dx = \frac{1}{2}e + \frac{1}{2}.

  10. 3. f(x) = ex + e−x, alors :

    003x
    • ∫01f(x)dx=e−1e+1\int_{0}^{1}f(x)dx = e − \frac{1}{e} + 1.
    • ∫01f(x)dx=e−1e−1\int_{0}^{1}f(x)dx = e − \frac{1}{e} − 1.
    • ∫01f(x)dx=e−1e\int_{0}^{1}f(x)dx = e − \frac{1}{e}.

  11. 4. f(t) = cos(2t + π3\frac{π}{3}), alors :

    001x
    • ∫0π3f(t)dt=−34\int_{0}^{\frac{π}{3}}f(t)dt = −\frac{\sqrt{3}}{4}.
    • ∫0π3f(t)dt=−14\int_{0}^{\frac{π}{3}}f(t)dt = −\frac{1}{4}.
    • ∫0π3f(t)dt=0\int_{0}^{\frac{π}{3}}f(t)dt = 0.

  12. D. Dans chaque question I = ∫03f(x)dx\int_{0}^{3}f(x)dx et C est la courbe représentative de f.

    1. 17000_grapheD1

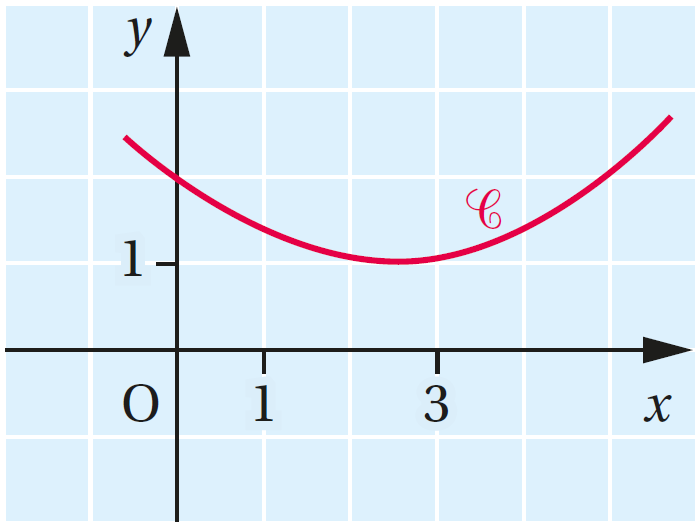
    Le nombre I appartient à :

    003x
    • [0, 3].
    • [6, 7].
    • [3, 5].

  13. 2. 17000_grapheD2.

    Le nombre I appartient à :

    002x
    • [0, 3].
    • [−3, 0].
    • [−1, 0].
Score : 10 1